Ongoing projects
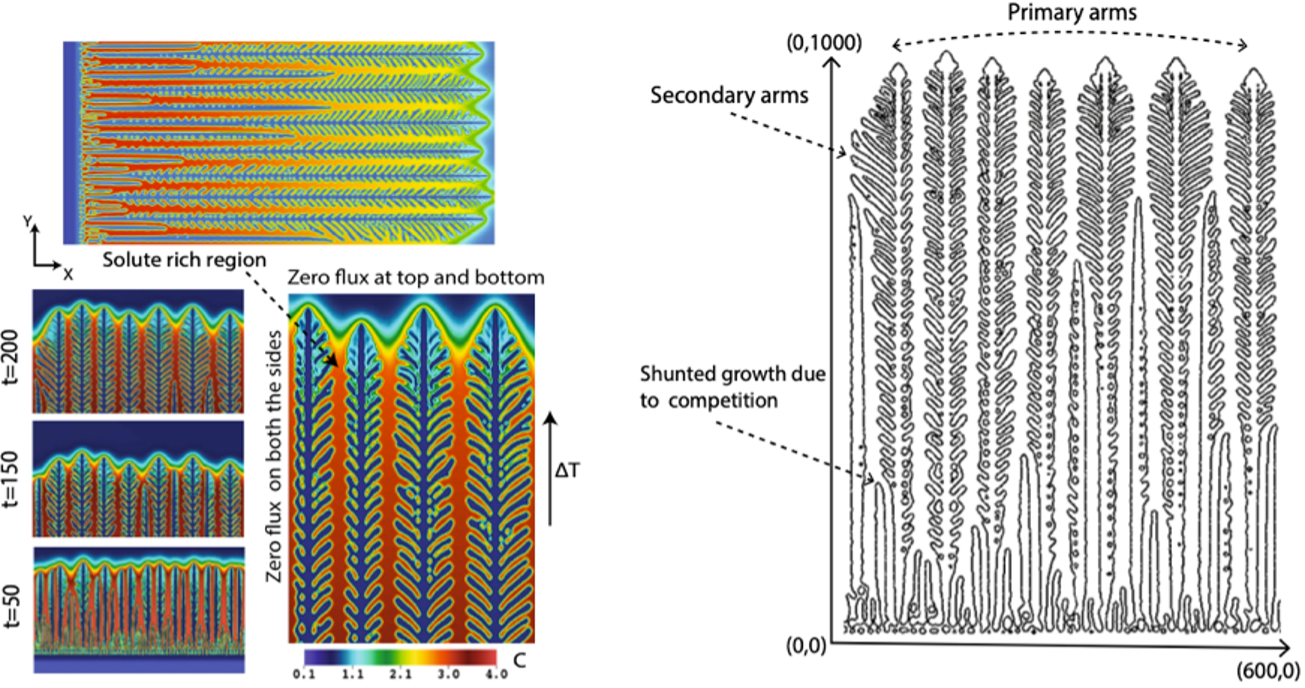
Microstructure modeling of dendritic and grain evolution in additively manufactured (AM) Nickel-based superalloys
This project seeks to model dendritic evolution and grain growth in Nickel-based alloys to produce high fidelity microstructural information that can be used in a multi-scale framework to estimate mechanical performance of AM printed parts.
Graduate students: Pratyusa Kar. In collaboration with Prof. Xiaoping Qian. Funded by ONR.
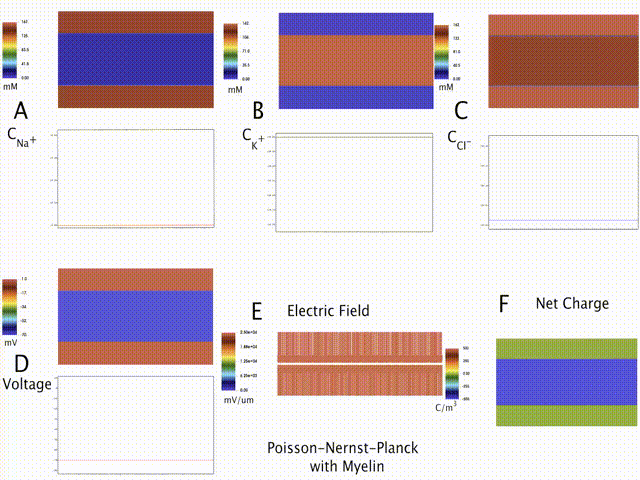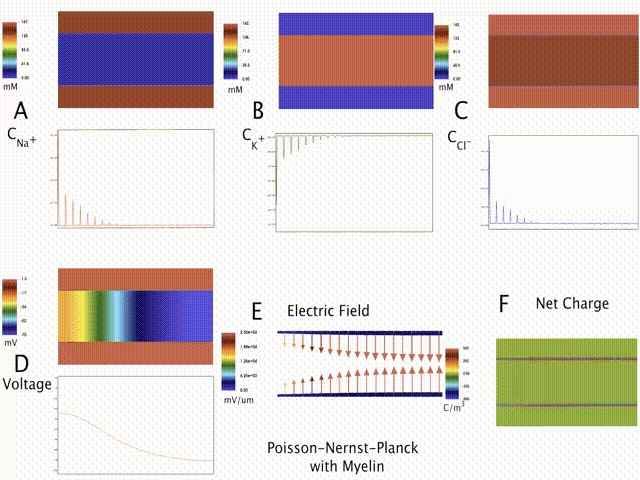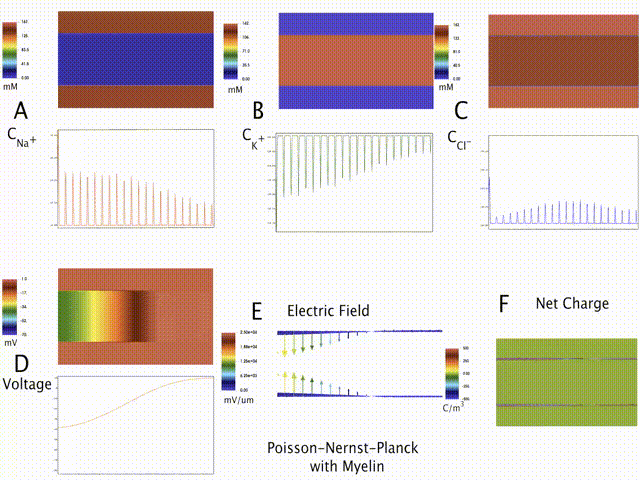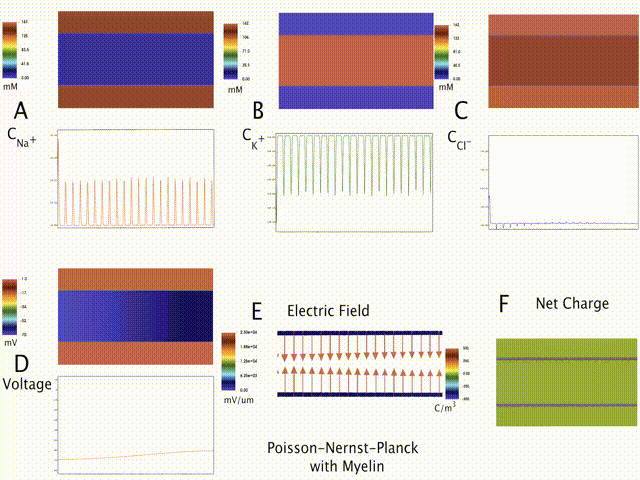
Multiphysics modeling of mechano-electro-chemistry underlying Traumatic Brain Injury
Electrical conduction in nerve cells is critical to the entire signaling and communication cascade of the nervous system. Disruption of this signaling can lead to a number of neurological disorders and is hypothesized to be one of the causes for Traumatic Brain Injury (TBI), Alzheimer's disease, etc. As part of our modeling work on the multiphysics basis of TBI, a Poisson-Nernst-Planck formulation based electro-diffusive framework that models the neuron-scale ionic transport and action potential propagation (AP) is developed. Further, we apply this spatio-temporal model to numerically estimate AP conduction velocity in rat and squid axons.
Graduate students: Sudip Kunda, Pratyusa Kar, Rahul Gulati and Debabrata Auddya. In collaboration with Prof. Christian Franck. Funded by ONR under the PANTHER program.
D. Auddya, S. Rudraraju,``Spatio temporal modeling of biomarker expression in neuronal clusters during traumatic brain injury'', (under review)
R. Gulati, S. Rudraraju,``Electro-diffusive modeling and the role of spine geometry on action potential propagation in neurons'', (under review) [arXiv]
R. Gulati, S. Rudraraju, "Spatio-temporal modeling of saltatory conduction in neurons using Poisson-Nernst-Planck treatment and estimation of conduction velocity", Brain Multiphysics, 100061, 2022. [journal] [arXiv]

Stability and evolution of microstructures - modeling grain growth in nanocrystalline alloys and phase transformation in intermetallics
We model the process of phase transformation in intermetallic alloys; specifically crystalline to amorphous transition and its relation to the stability of underlying lattice structure. The project focus is on deriving an improved theoretical estimate of the onset of instability in metallic alloys. Onset of instability is numerically demonstrated and compared with predictions of MD simulations.
In the context of nanocrystalline alloys, we model grain level phenomena linked with contact driven mechanical deformation. The three key phenomena being modeled are microstructure evolution, elasto-plastic deformation of the multi-grain aggregates, and contact modeling of the interface friction.
Graduate student: Prakarsh Pandey. In collaboration with Prof. Izabela Szlufarska (MSE). Funded by ARO.
P. Pandey, S. Rudraraju, "Phase field formulation of nanocrystalline grain evolution and solute drag effects", (under review)[Preprint]
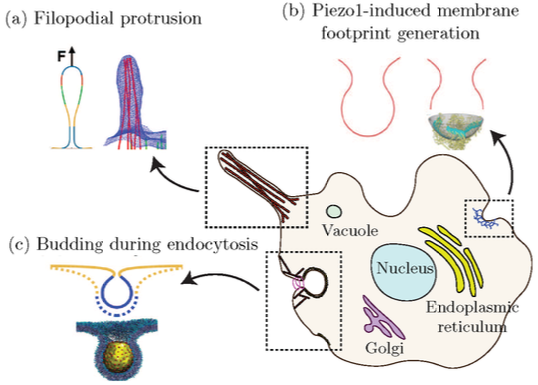
Membrane Mechanics and Multiphysics Underlying Complex Electro-Chemo-Mechanical Response of Biomembranes
Various biomembrane bound phenomena are central to the functioning of biological cells and play a key role in many disease conditions. Thus, an understanding of the physical interactions active on the surface of biomembranes is important to develop a deeper appreciation of cell functioning, and their implications on human health and disease conditions. The work aims to develop a novel theoretical formulation that models membrane deformation and its interactions with transport and electrochemical processes. The distinguishing aspect of this work is the strong integration of multiphysics (membrane mechanics, surface transport and surface electrochemistry) to enable a unified treatment of various coupled phenomena in biomembranes.
Graduate students: Pratyusa Kar and Rahul Gulati. Funded by NSF.

Microstructure evolution during solidification
Dendrites are one of the most widely observed patterns in nature, and occur across a wide spectrum of physical phenomena—from snowflakes to bacterial colonies to solidification patterns in crystals. As part of our metal Additive Manufacturing modeling work, we developed a comprehensive numerical treatment for modeling various Stefan problem formulations of dendritic evolution using a phase-field approach. The distinguishing aspects of this work are - a unified treatment of both pure metals and alloys; numerical error estimates of dendritic velocity; and study of error convergence.
Graduate student: Kunal Bhagat.
K. Bhagat, S. Rudraraju, "Modeling of dendritic solidification and numerical analysis of the phase-field approach to model complex morphologies in alloys", Engineering with Computers (EWCO), 2022. [journal] [arXiv]
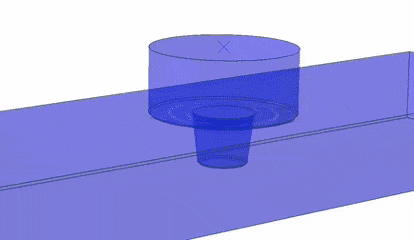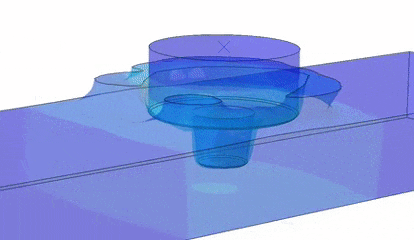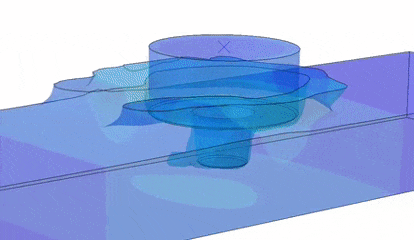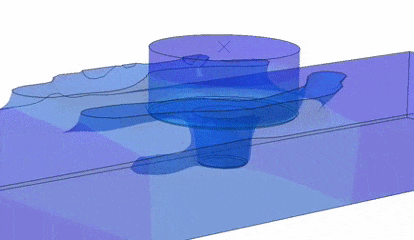
Intermittent material flow during friction stir welding (FSW)
Friction Stir Welding is a relatively new solid-state welding process that has significant advantages over conventional fusion processes. We model plastic flow induced by the underlying thermo-mechanical processes and seek to gain a fundamental understanding of how and when defects (voids) are formed, and identify process parameters that allow for optimal control over the properties of the resulting weld.
Graduate student: Mohammad Ansari. In collaboration with Prof. Frank Pfefferkorn and Prof. Mike Zinn. Funded by NSF.
Past projects

Dimensional analysis of meltpool thermo-fluidic evolution during metal additive manufacturing
Microstructure evolution in metal additive manufacturing is a complex multi-physics and multi-scale problem. In this work, a novel strategy using dimensional analysis and the method of linear least-squares regression is used to numerically investigate the thermo-fluidic governing equations of the Laser Powder Bed Fusion process. Through dimensional analysis, an important dimensionless quantity - interpreted as a measure of heat absorbed by the powdered material and the meltpool, is identified. This dimensionless measure of heat absorbed, along with classical dimensionless quantities such as Péclet, Marangoni, and Stefan numbers, is used to investigate advective transport in the meltpool for different alloys.
Graduate student: Kunal Bhagat.
K. Bhagat, S. Rudraraju, "A numerical investigation of dimensionless numbers characterizing meltpool morphology of the laser powder bed fusion process", Materials, 2022. [journal] [Preprint]
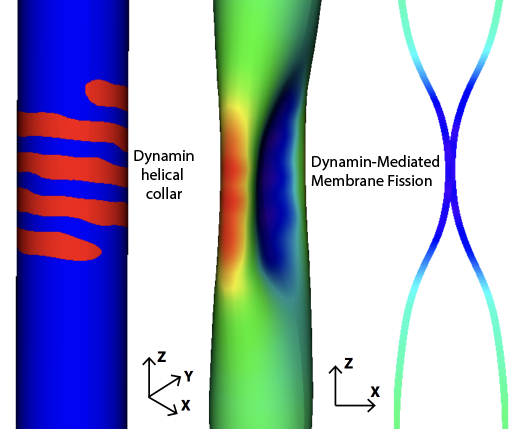
Modeling instabilities in biological membranes using Kirchhoff-Love shell kinematics
The formation and constriction of membrane necks as a precursor to membrane fission is a fundamental step for a variety of biological processes including endocytosis, cytokinesis, etc. Using a curvilinear coordinates based Kirchhoff-Love thin shell kinematics framework, we model the deformational response and instabilities in various membrane geometries, study the suitability of Helfrich like material models, and determine the boundary conditions needed to induce preferred deformation modes.
Graduate student: Debabrata Auddya and Rahul Gulati. In collaboration with Prof. Padmini Rangamani (UCSD) and Prof. Krishna Garikipati (UM).

Modeling embryogenesis as soft packing of multi-cell aggregates driven by growth and cell division
Formation of multi-cell aggregates is a foundational process in the evolution of multicellular organisms. Beginning with a single cell or a small cluster, the growth of aggregates is driven by cell division, differentiation, migration and cell-cell interactions. Understanding the processes underlying the formation of these aggregates is central to many phenomena in cellular biology and physiology, including embryogenesis, wound healing and tissue engineering. In this work, we develop a model for cell growth, division and packing under soft constraints that arise from the deformability of the cells as well as of a membrane that encloses them. Our treatment falls within the framework of diffuse interface methods, under which each cell is represented by a scalar phase field and the zero level set of the phase field represents the cell membrane.
In collaboration with Prof. Krishna Garikipati (UM).
J. Jiang, K. Garikipati, S. Rudraraju``A diffuse interface framework for modelling the evolution of multi-cell aggregates as a soft packing problem due to growth and division of cells'', Bulletin of Mathematical Biology , 2019. [journal][arXiv]
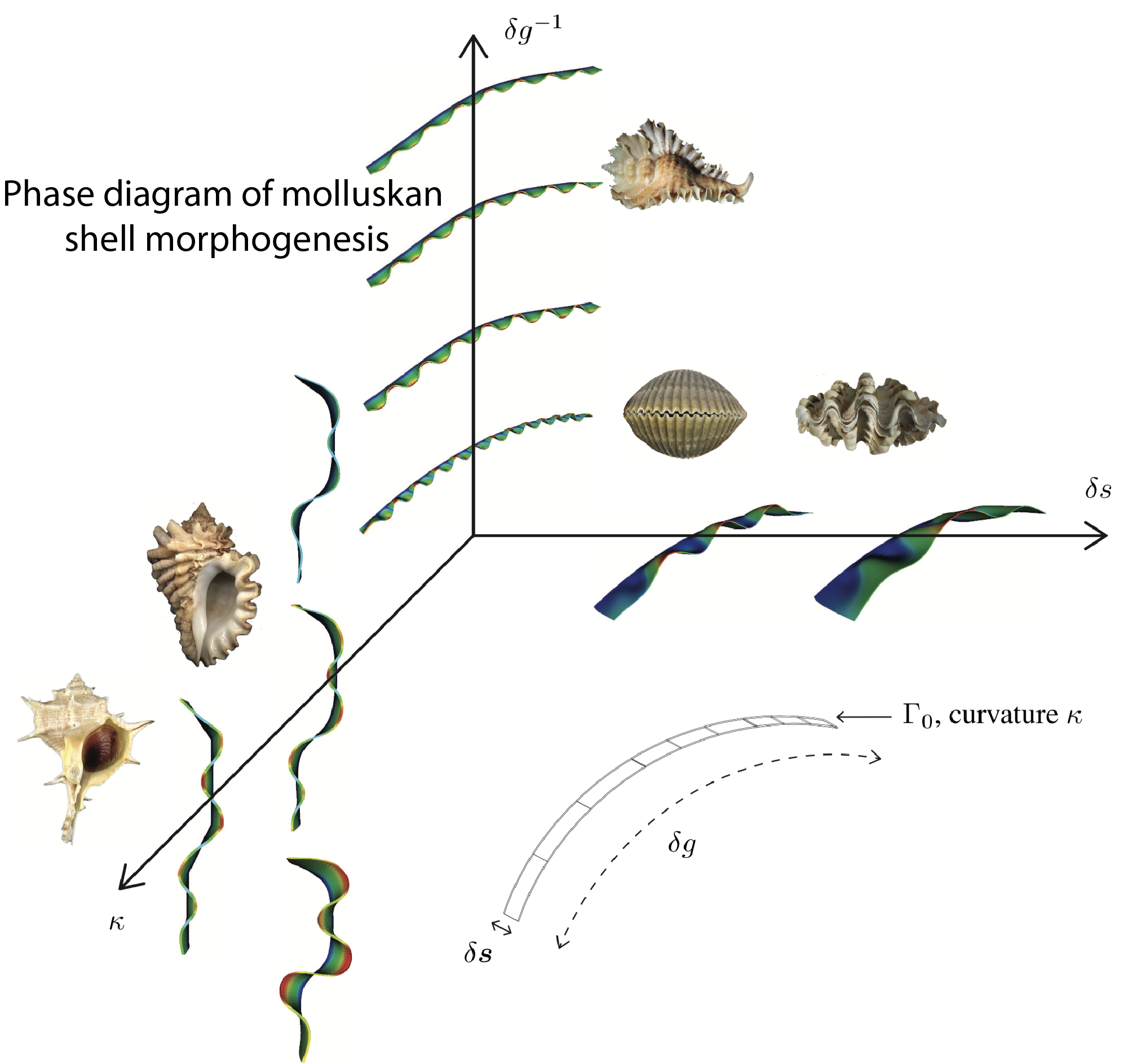

Mechanical basis of morphogenesis: Morpho-elastic development of molluskan shells
Molluskan shells are an important model system for understanding mechano-morphological basis of the evolution of exoskeleton in invertebrates. Here we propose a three-dimensional computational framework coupling morphology, incremental surface growth by accretion, and morpho-elastic volume growth, to enable an improved representation of the growth and structural parameters controlling the evolution of shell structural ornamentations. We study the effects of growth rates, and of previously deposited shell geometries on the resulting modes of mantle deformation, and determine a ``phase diagram'' of morphogenesis in molluskan shells. Our main motivation for focusing on generic physical processes involved in development is that they may shape living beings in a predictive way and partly determine the spectrum of forms that have been and could have been generated during evolution.
In collaboration with Derek Moulton (Oxford), Alain Goriely (Oxford) and Krishna Garikipati (UM).
S. Rudraraju, D.E. Moulton, R. Chirat, A. Goriely, K. Garikipati, ''A computational framework for the morpho-elastic development of molluskan shells by surface and volume growth'', PLOS Computational Biology, 15(7): e1007213, 2019. [journal][arXiv]
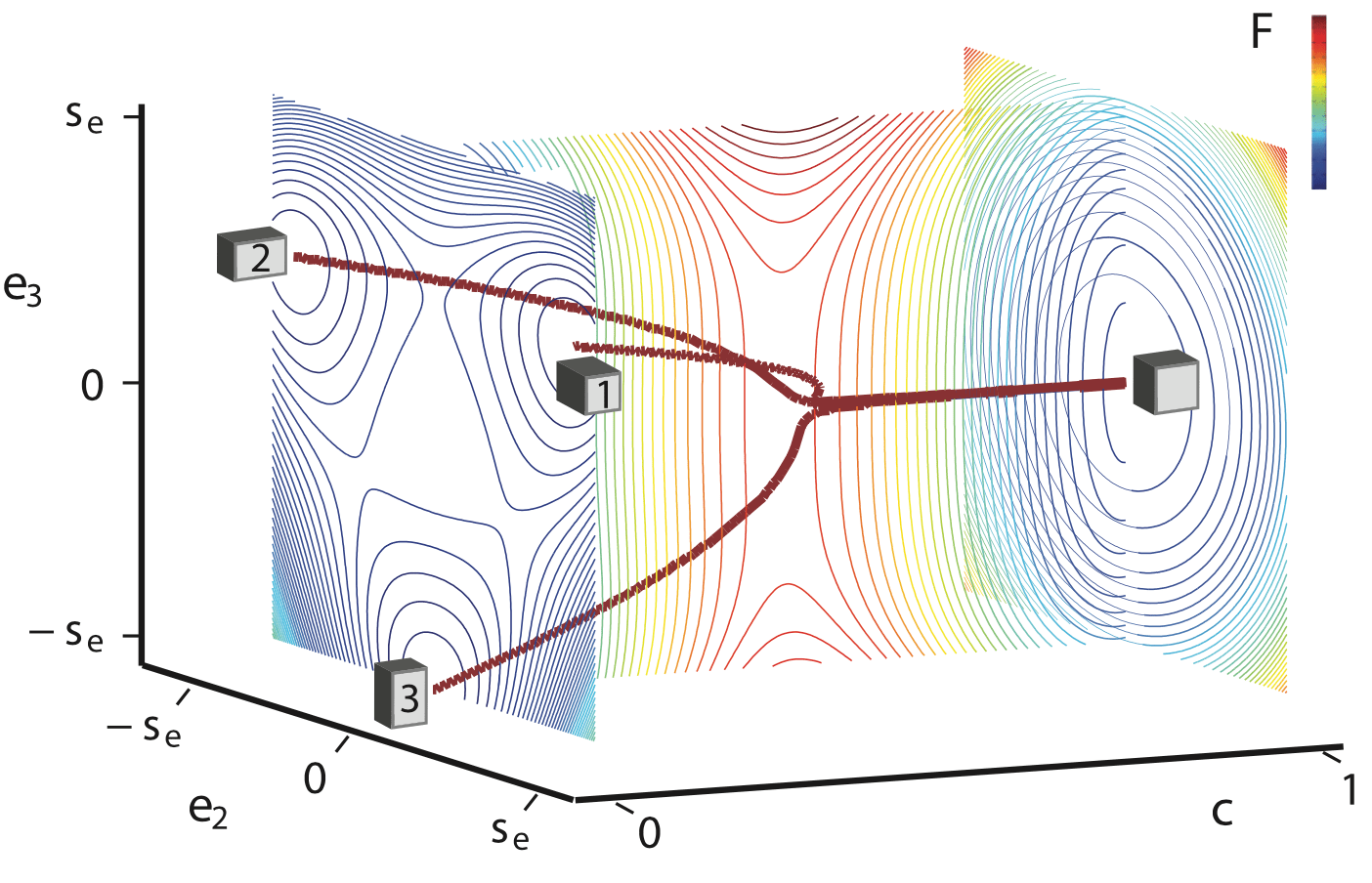

Mechanochemical spinodal decomposition in multi-component solids
We present a phenomenological treatment of diffusion driven martensitic phase transformations in multi-component crystalline solids that arise from non-convex free energies in mechanical and chemical variables. The treatment describes diffusional phase transformations that are accompanied by symmetry-breaking structural changes of the crystal unit cell and reveals the importance of a mechanochemical spinodal, defined as the region in strain–composition space, where the free-energy density function is non-convex. The approach is relevant to phase transformations wherein the structural order parameters can be expressed as linear combinations of strains relative to a high-symmetry reference crystal. Specifically, phase transformations in shape memory alloys, electrode materials for Li-ion batteries and certain high-temperature ceramics are of interest.
In collaboration with Krishna Garikipati (UM) and Anton Van der Ven (UCSB).
S. Rudraraju, A van der Ven, K. Garikipati, ``Mechano-chemical spinodal decomposition: A phenomenological theory of phase transformations in multi-component, crystalline solids'', Nature npj Computational Materials, 2016, doi:10.1038/npjcompumats.2016.12. [journal] [arXiv]
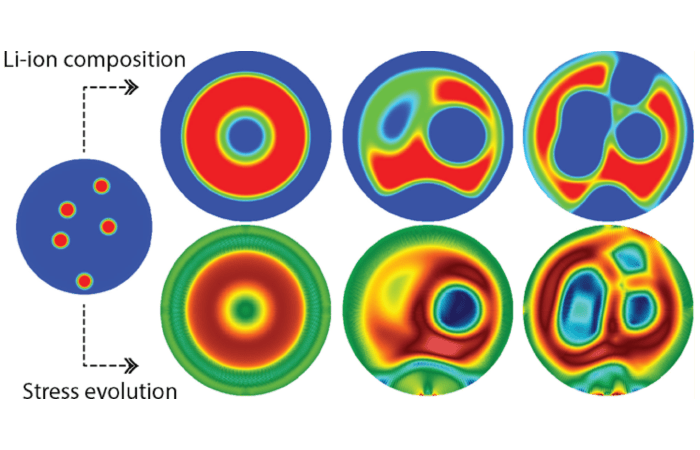
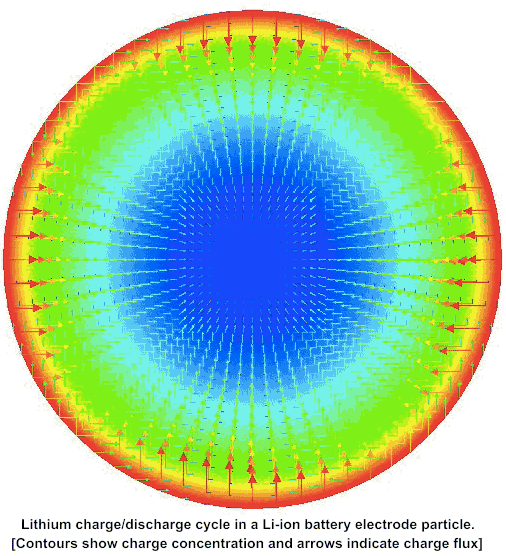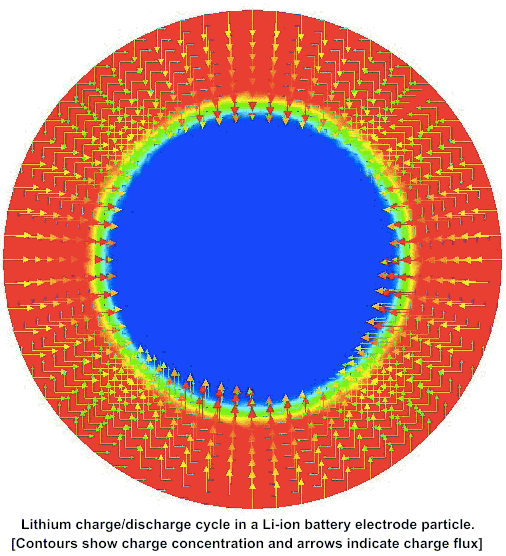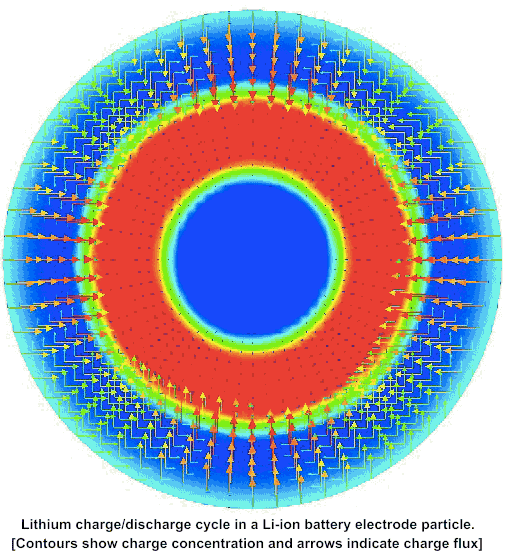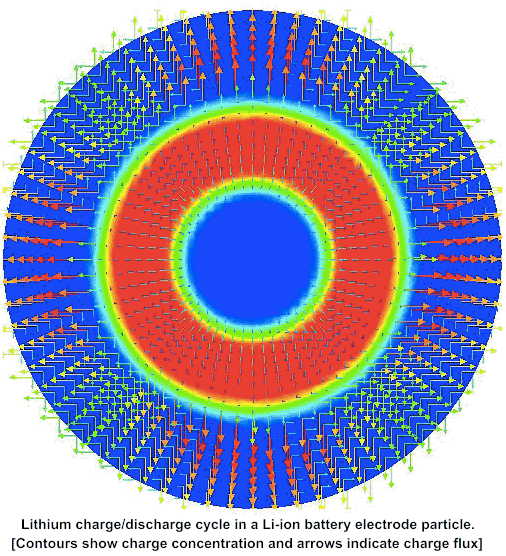
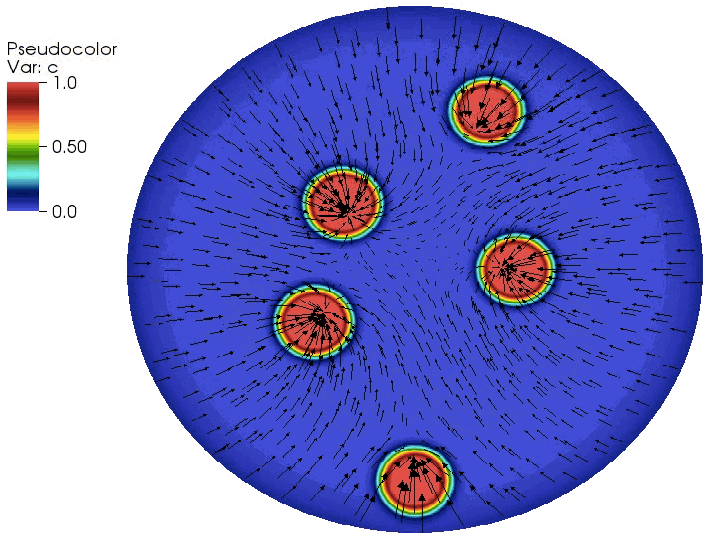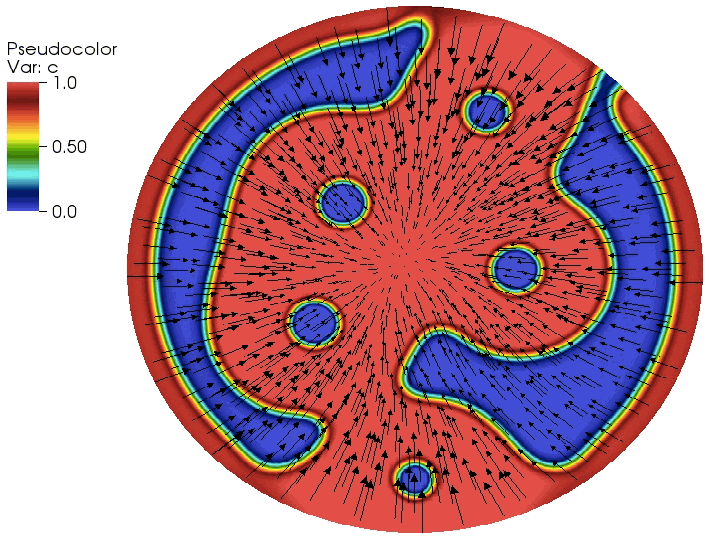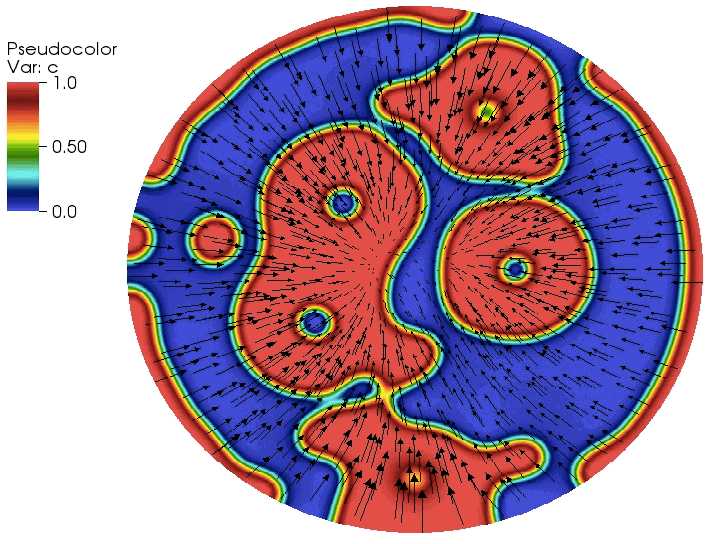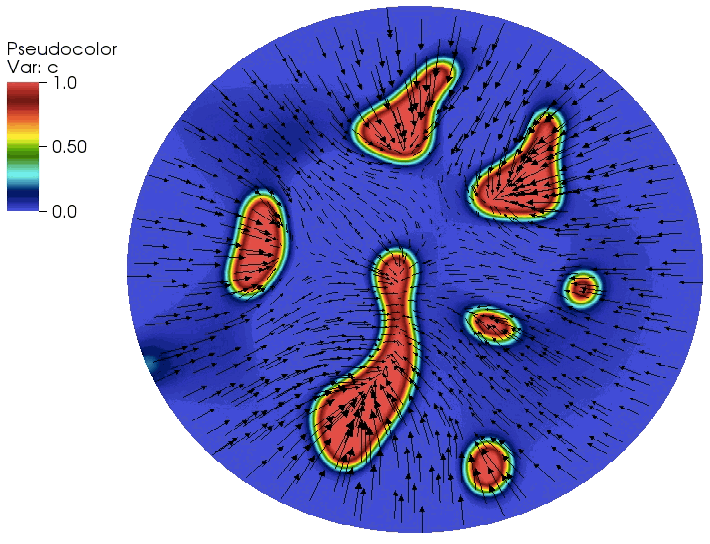
Multiphysics simulations of diffusion induced stress in Lithium ion battery electrode particles
Cubic spinel LiTiO is a promising electrode material because it exhibits a high lithium diffusivity and undergoes minimal changes in lattice parameters during lithiation and delithiation, thereby ensuring favorable cyclability. This work is a multiphysics and multiscale study of LiTiO that combines first-principles computations of thermodynamic and kinetic properties with continuum scale modeling of lithiation−delithiation kinetics. Several case studies explore the temporal evolution of peak stresses and the potential for crack initiation, during lithiation and delithiation.
In collaboration with Krishna Garikipati (UM) and Michael Falk (JHU).
T. Jiang, S. Rudraraju, A. Roy, A. Van der Ven, K. Garikipati, M. L. Falk, ``Multi-physics simulations of lithiation-induced stress in LiTiO electrode particles'', Journal of Physical Chemistry C, 2016, [journal] [arXiv]


Intrinsic length scale in gradient elasticity and its effect on cracks, dislocations and microstructure
Classical elasticity is scale invariant: it does not admit length scales intrinsic to the material. The only length scale which may manifest itself arises from the problem geometry. However, real materials do posses intrinsic length scales (i.e., interatomic distance, dislocation cells, grain sizes, etc). If the deformation varies on these scales, size effects may arise. One framework that is appropriate for treating such problems is the strain gradient formulation of elasticity. We have developed a comprehensive numerical framework for Toupin’s theory of nonlinear gradient elasticity and obtained the first complete three-dimensional numerical solutions to a broad range of boundary value problems in gradient elasticity at finite strain. The governing equation is a fourth order partial differential equation with complex boundary conditions. Studies conducted using the framework include gradient length scale effects on microscale/nanoscale structural problems, regularization of crack tip solutions and modeling of mechanically induced microstructure.
In collaboration with Krishna Garikipati (UM) and Anton Van der Ven (UCSB).
S. Rudraraju, A van der Ven, K. Garikipati, ``Three-dimensional iso-geometric solutions to general boundary value problems of Toupin's gradient elasticity theory at finite strains'', Computer Methods in Applied Mechanics and Engineering (CMAME), Vol 278, Pages 705-728, 2014. [journal][arXiv]
Z. Wang, S. Rudraraju, K. Garikipati,``A three dimensional field formulation, and isogeometric solutions to point and line defects using Toupin's theory of gradient elasticity at finite strains'', Journal of the Mechanics and Physics of Solids (JMPS), Vol. 94: 336-361, 2016, doi:10.1016/j.jmps.2016.03.028.[journal][arXiv]
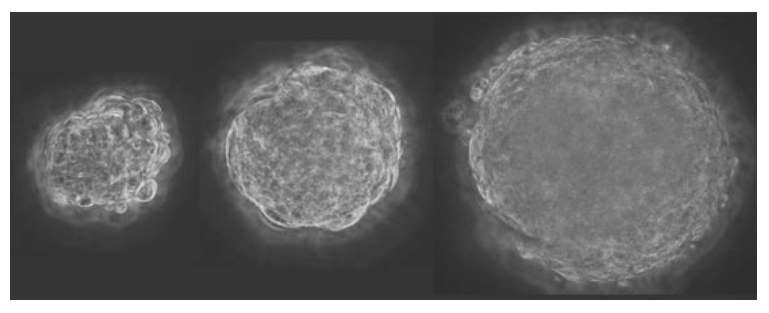
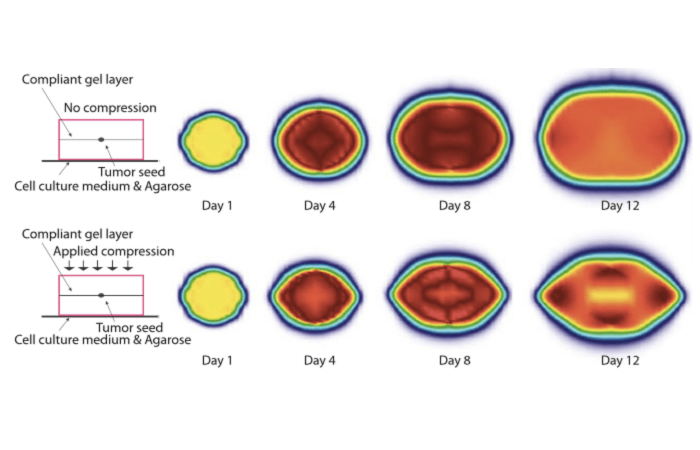
The continuum physics of tumor growth
The dynamical processes of chemistry, transport and mechanics that govern tumor growth can be broadly classified into three distinct spatial scales: the tumor scale, the cell-extracellular matrix (ECM) interactions and the sub-cellular processes. In this work, we focus on tumor scale investigations, and model the emergent morphology of tumors to gain system-level insights into their progression. The evolution of various constituents (cancer cells, stem cells, necrotic cells, nutrients, byproducts, etc) is modelled with reaction-advection-diffusion equations coupled with finite strain mechanics.
In collaboration with Kristen Mills (Max Planck Institute for Intelligent Systems, now at RPI), Ralf Kemkemer (Max Planck Institute for Intelligent Systems) and Krishna Garikipati (UM)
S. Rudraraju, K.L.Mills, R Kemkemer, K. Garikipati, ``Multiphysics Modeling of Reactions, Mass Transport and Mechanics of Tumor Growth'' Computer Models in Biomechanics, Pages 293-303, 2013. [journal]
K.L.Mills, R Kemkemer, S. Rudraraju, K. Garikipati, ``Elastic free energy drives the shape of prevascular solid tumors'', PLoS ONE, 9(7), 2014. [journal] [arXiv]
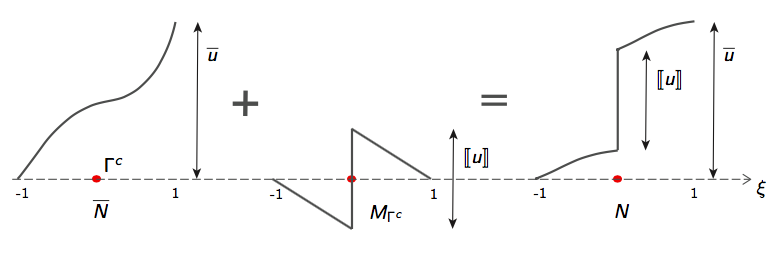


Micromechanics and crack propagation in laminated fiber reinforced composites
Modeling crack propagation in fiber reinforced composites is more challenging than conventional brittle/ductile materials due to the presence of large process zones behind the crack tip. These process zones, also known as bridging zones or cohesive zones, are regions of complex fiber-matrix micromechanics which significantly enhance the fracture toughness. To address this modeling problem, we developed a numerical framework for cohesive crack propagation based on the variational multiscale method. It treats cracks as displacement discontinuities and represents them as fine scale variations with compact support on a coarse scale displacement field. This treatment leads to a multiscale model with a coarse scale problem enforcing the conservation of linear momentum and a fine scale problem representing the micromechanics (cohesive surface laws).
S. Rudraraju, A. Salvi, K. Garikipati, A. M. Waas, ``In-Plane fracture of laminated fiber reinforced composites with varying fracture resistance: experimental observations and numerical crack propagation simulations'', International Journal of Solids and Structures (IJSS), Vol 47, Issues 7-8, Pages 901-911, 2010. [journal] [arXiv]
S. Rudraraju, A. Salvi, K. Garikipati, A. M. Waas, ``Predictions of crack propagation using a variational multiscale approach and its application to fracture in laminated fiber reinforced composites'', Composite Structures, Vol 94, Issue 11, Pages 3336-3346, 2012. [journal]
S. Rudraraju, A. Salvi, K. Garikipati, A. M. Waas, ``Experimental observations and numerical simulations of curved crack propagation in laminated fiber composites'' Composites Science and Technology (CST), Vol 72, Issue 10, Pages 1064-1074, 2012. [journal]
S. Rudraraju, K. Garikipati, A.M. Waas, B.A. Bednarcyk, ``On the Theory and Numerical Simulation of Cohesive Crack Propagation with Application to Fiber-Reinforced Composites'', NASA Technical Publication (peer reviewed) (NASA/TP-2013-217431, E-18123), 2013. [NASA Archive]