In a nutshell...
We model emergent phenomena in materials (structural and biological) that are driven by mechanics and multiphysics. Microstructural evolution, patterning processes and bifurcations are of special interest.
This work draws heavily from solid mechanics, continuum physics, thermodynamics and uses a spectrum of numerical methods and scientific computing platforms.
For details about ongoing and past projects, please look at the Research page.
Open positions: Two potential PhD/PostDoc positions open for Spring 2025/Fall 2025 on (1) multiphysics modeling of biological systems (NSF and ONR funded) and (2) microstructure modeling in metal Additive Manufacturing (ONR funded). Both positions focus on extensive computational mechanics and multiphysics modeling, and involve modeling phenomena across length scales. Prospective students with interest in numerical modeling, solid mechanics, multiphysics and/or biomechanics may email CV's to shiva dot rudraraju at wisc dot edu
Broad themes

Morphology evolution in biological systems
Continuum treatment of various mechanics and multiphysics driven biological phenomena at the cellular scale (e.g. neuronal mechanics modeling, membrane processes like endocytosis, embryogenesis, etc.). This work requires coupling of mechanics, transport and electrostatic processes, often on surface manifolds, and involves study of instabilities and structural bifurcations.
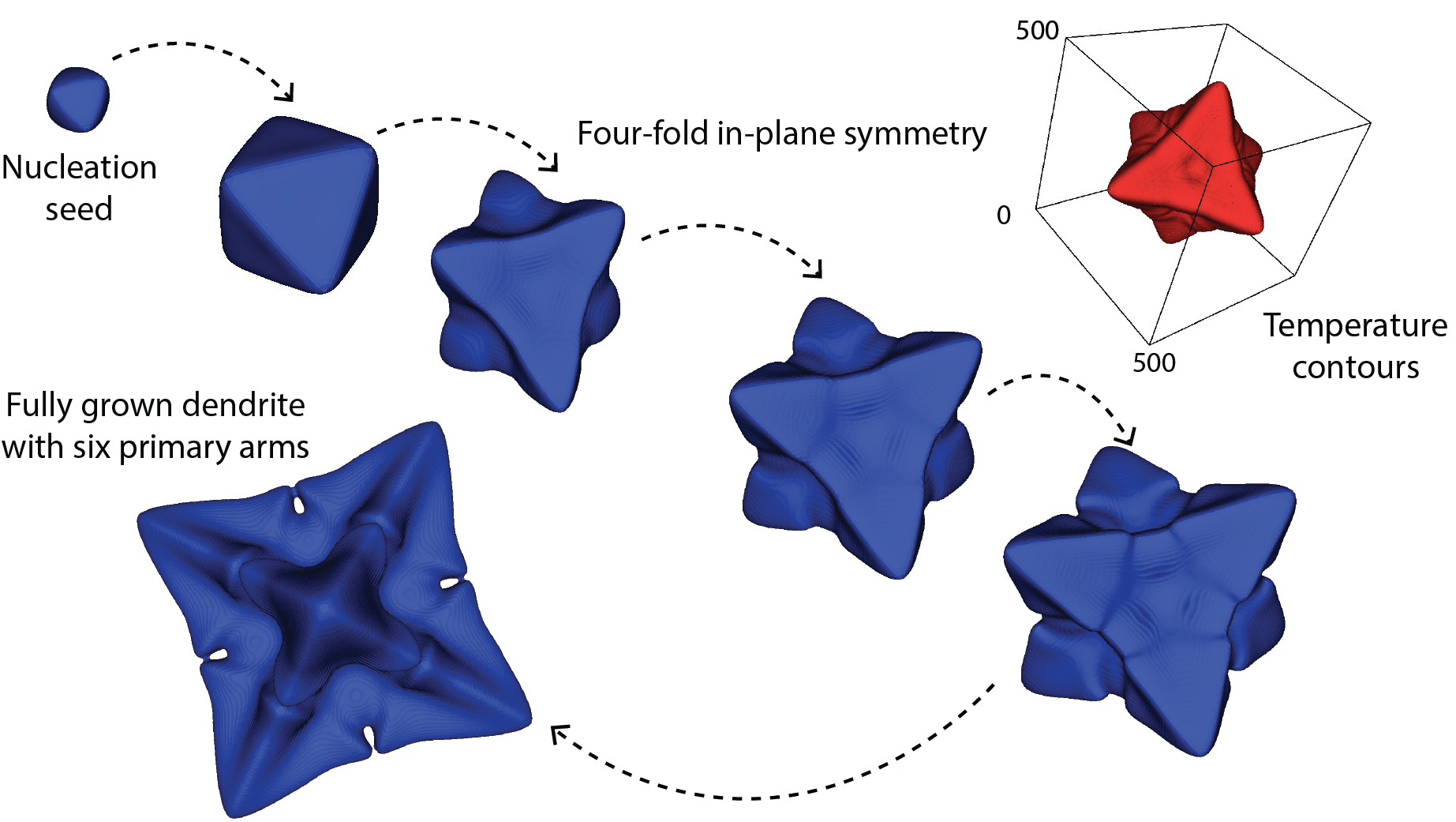
Microstructure evolution in manufacturing processes
Mesoscale modeling of mechanical deformation and microstructure evolution in manufacturing processes like Friction Stir Welding and Additive Manufacturing. This work involves modeling of the thermo-mechanics, formation of voids/defects, and evolution of microstructure (dendrites and grains).
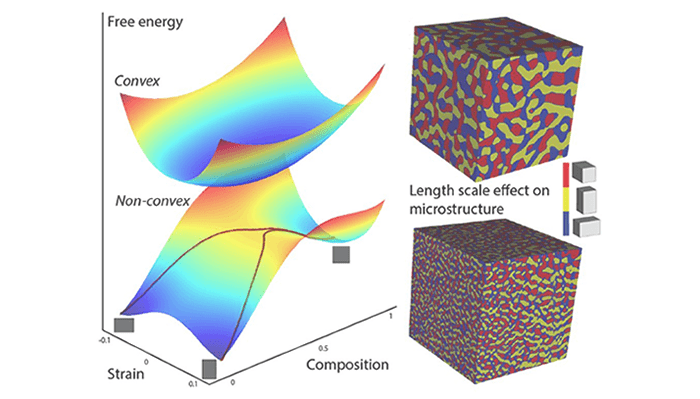
Phase transformations and stability of alloys
Theoretical and numerical modeling of elastic stability conditions (e.g. for crystalline to amorphous transformations, for martensitic transformation, etc.) and phase transformations in metallic alloys and functional materials.
- Theoretical elastic stability conditions for intermetallic alloys
- Microstructure evolution in nanostructured alloys
- Mechanochemical spinodal decomposition in multi-component solids
- Diffusion induced stress in Li-ion battery electrode particles
- Intrinsic length scale in gradient elasticity and its effect on cracks and dislocations
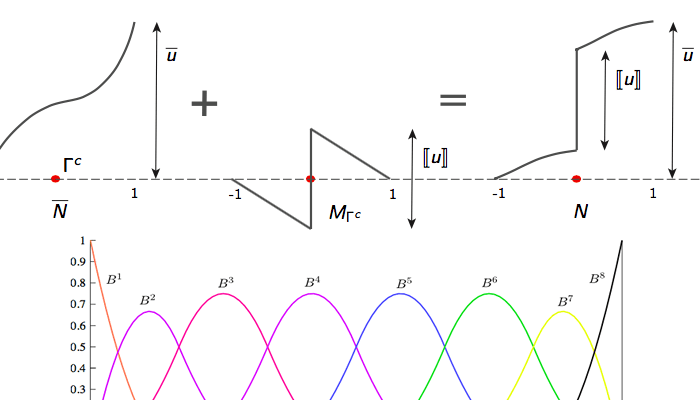
Numerical methods and scientific computing
Developing numerical formulations (FEM, IGA, FDM, etc) and scalable code infrastructure for modeling coupled PDE's. Also involves developing numerical frameworks for modeling contact, fracture and phase evolution.